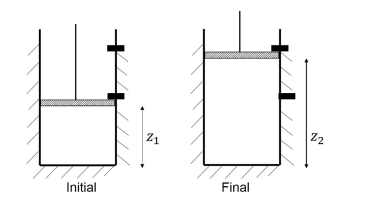
Consider a piston-cylinder assembly shown in the figure below. The walls of the cylinder are insulated. The cylinder contains $1$ mole of an ideal gas at $300 \; \text{K}$ and the piston is held initially at the position $\text{z}_{1}$ using a stopper. After the stopper is removed, the piston suddenly rises against atmospheric pressure $(1.013\times 10^{5} \; \text{Pa})$ to the new position $\text{z}_{2}$ where it is held by another stopper.
The heat capacity $(C_{v})$ of the gas is $12.5 \; \text{J mol}^{-1} \text{K}^{-1}.$ The cross-sectional area of the cylinder is $10^{-3} \text{m}^{2}.$ Assume the piston is weightless and frictionless.
If $\text{z}_{2} – \text{z}_{1} =1\; \text{m},$ the final temperature of the gas (rounded off to nearest integer) is _____________$\text{K}.$