In the following diagram, the point $\text{R}$ is the center of the circle. The lines $\text{PQ}$ and $\text{ZV}$ are tangential to the circle. The relation among the areas of the squares, $\text{PXWR, RUVZ}$ and $\text{SPQT}$ is
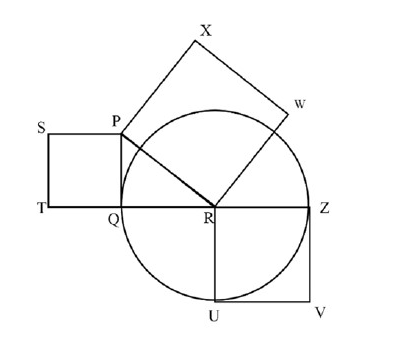
- Area of $\text{SPQT}$ = Area of $\text{RUVZ}$ – Area of $\text{PXWR}$
- Area of $\text{SPQT}$ = Area of $\text{PXWR}$ – Area of $\text{RUVZ}$
- Area of $\text{PXWR}$ = Area of $\text{SPQT}$ – Area of $\text{RUVZ}$
- Area of $\text{PXWR}$ = Area of $\text{RUVZ}$ – Area of $\text{SPQT}$